t2
= 2Zt.
The weight for Weighted Least Squares (WLS) is inversely proportional to
the variance of the error terms. Therefore wt = 1 / Zt.
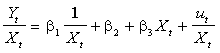
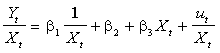
Multiply each variable by the square root of wt and use
the transformed variables in the regression.
1
+ 2
Xt + 3Xt2
+ ut by Xt. We get
2
and not for 1.
Yt
= 1
+ 2Xt2+ 3Xt3
+ ut
.
Var (ut)
= wt Var(ut) = nt ( 2
/ nt ) = 2.
Therefore OLS applied to the transformed model will give estimates that
are BLUE. Thus, we would regress Yt
against , Xt2,
and Xt3,
with no constant term.
t2
= 
Pt,
we get ln(t2)
=
ln
+
lnPt, The null hypothesis is
= 0 and the alternative is that it is not zero. The auxiliary equation
in this case is ln(t2)
= ln
+
lnPt, To compute the test statistic, (1) regress Et
against a constant and Yt, (2) save the residual 
,
(3) regress ln(
)
against a constant and ln(Pt), and (4) compute LM = N
R2, the product of the number of observiations and the unadjusted
R2
from step 3. Under the null hypothesis of homoskedasticity, LM has an asymptotic 
2
distribution with one d.f. The steps to get more efficient estimates are
as follows:
1. Regress Et against a constant and Yt.
2. Save the residual .
3. Regress ln()
against a constant and ln(Pt) and then compute 
and 
from
it.
4. Estimate t2
by 
5. Compute the weight as wt = 1 /
6. Obtain WLS estimates by regressing Et
against and Yt
with no constant term.
t2
= 1
+ 2St
+ 3Dt
+ 4St2
+ 5
(St ×Dt). Dt2
is not included because there is an exact linear relation with Dt,
which is a dummy variable.
b. 2
= 3
= 4
= 5
= 0.
c. Regress Pt against a constant, St,
and Dt and obtain 
Next regress against
a constant, St, Dt, St2,
and (St ×Dt).
d. Under the null hypothesis, the test statistic N R2
is distributed asymptotically as 2
with 4 d.f.
e. The critical value of 2
with 4 d.f. at 5 percent is 9.48773. Reject the null if N R2
is greater than this.
f. Take the calculated values of the second regression in (c) {regressing against
a constant, St, Dt, St2,
and (St ×Dt)}. Use these calculated
values as an estimateof
the value of t2
to be obtained from the auxiliary regression in (a). Compute the WLS weight
wt
= 1 /.
Finally, regress Pt
against , St,
and Dt
without a constant term.
2
= 3
= 0. H1: at least one is not zero.
;
(3) regress against
a constant, Pt , and Pt2.
c. Compute N R2 from the regression in Step 3 of part b above.
d. Under H0 this statistic has an asymptotic 2
distribution with 2 d.f.
e. Take the calculated values of the regression in Step 3 of (b) above,
and use these calculated values as an estimateof
the value of t2
to be obtained from the auxiliary regression. If is
not positive for any t, then either drop that observation or use for
that t. Compute the WLS weight wt = 1 /.
Finally, regress Et
against
and Yt
without a constant term.
t2
= k YARDt. Multiply each variable (including the
constant) by 1/
YARDt
and regress PRICEt/YARDt
against
1/YARDt,
ln(SQFTt) /YARDt
,
and ln(YARDt) /YARDt
.
b. Since the weights are known, the WLS estimates are BLUE whereas the OLS estimates are not.
c. e.g., t
= 1
+ 2
SQFTt + 3
YARDt .
d. H0: 2
= 3
= 0.
e. First regress PRICE against a constant, ln(SQFT), and ln(YARD) and
compute the residuals 
.
Next, estimate the auxiliary equation in (c) by regressing |
|
against a constant, SQFTt , and YARDt
and compute LM = N R2. Under H0 this
statistic has an asymptotic 2
distribution with 2 d.f..
f. Estimate t
by 
.
Regress PRICEt /
against 1 /,
ln(SQFTt) /
and ln(YARDt) /
with no constant term.
t2
= 2
/ Nt , and the weight for Weighted Least Squares
(WLS) is inversely proportional to the variance of the error terms,wt
= 1 / Zt. Multiply each variable (including the constant
term) by the square root of wt and use the transformed
variables in the regression. Because the weights are known, WLS estimates
are unbiased,consistent, and BLUE. Tests of hypotheses are valid.
t2
= 1
+ 2LSt
+ 3Dt
+ 4LSt2
+ 5
(LSt ×Dt). Dt2
is not included because there is an exact linear relation with Dt,
which is a dummy variable.
b. 2
= 3
= 4
= 5
= 0.
c. Regress LPt against a constant, LSt,
and Dt and obtain 
.
Next regress against
a constant, St, Dt, St2,
and (St ×Dt).
d. Under the null hypothesis, the test statistic N R2
is distributed asymptotically as 2
with 4 d.f.
e. The critical value of 2
with 4 d.f. at 5 percent is 9.48773. Reject the null if N R2is
greater than this.
f. The OLS estimates are unbiased and consistent, but not efficient.
Updated March 9, 2000
noelroy@morgan.ucs.mun.ca