Serial Correlation Exercises
Exercise 9.2
The estimated model is based on cross-section data. Therefore, the
serial
correlation test is meaningless.Cross-section data can always be
rearranged
to get different values for the DW statistic.
Exercise 9.3
According to Table A.5 of the textbook, dL = 1.24
for
n
= 27 and k' = 2. Since d = 0.65 < dL
, we can reject the null hypothesis of no first-order serial
correlation
against the alternative of positive first-order serial correlation.
Since
the independent variables are exogenous, the parameter estimates and
forecasts
are unbiased. However, standard errors and t-values are
incorrect
and the goodness of fit is generally exagerated (because the estimate
of
the variance of the disturbances is biased downward). Hypothesis tests
are invalid as a result. An alternative method is the Cochrane-Orcutt
procedure
for FGLS estimation, as outlined on p. 446 of the textbook. For a
correct
value of  ,
GLS
estimation results in Best Linear Unbiased estimates (BLUE) of the
equation
parameters. When a consistent estimator of
,
GLS
estimation results in Best Linear Unbiased estimates (BLUE) of the
equation
parameters. When a consistent estimator of  is used instead of its true value, the estimates are asymptotically
efficient,
but not efficient in small samples relative to an estimator based on
the
true value of
is used instead of its true value, the estimates are asymptotically
efficient,
but not efficient in small samples relative to an estimator based on
the
true value of  .
.
Exercise 9.5
Let the assumption on the error terms be ut =  ut-1
+
ut-1
+  t
,
where
t
,
where  t
is
independently normally distributed. The null hypothesis is
t
is
independently normally distributed. The null hypothesis is  = 0, and the alternate hypothesis is
= 0, and the alternate hypothesis is  > 0. According to Table A.5 of the textbook, dL =
1.37
for
n = 32 and k' = 1. Since d = 0.207 < dL
, we can reject the null hypothesis of no first-order serial
correlation
against the alternative of positive first-order serial correlation.
Therefore,
we are not justified in feeling that the fit is excellent and the
regression
coefficients extremely significant. Serial correlation renders
hypothesis
tests invalid and generally results in goodness-of-fit statistics which
exagerate the true value.
> 0. According to Table A.5 of the textbook, dL =
1.37
for
n = 32 and k' = 1. Since d = 0.207 < dL
, we can reject the null hypothesis of no first-order serial
correlation
against the alternative of positive first-order serial correlation.
Therefore,
we are not justified in feeling that the fit is excellent and the
regression
coefficients extremely significant. Serial correlation renders
hypothesis
tests invalid and generally results in goodness-of-fit statistics which
exagerate the true value.
Exercise 9.6
a. ut =  ut-1
+
ut-1
+  t
. H0
:
t
. H0
:  = 0.
= 0.
b. Since k' = 4 and n = 41, dL
is in the range (1,285, 1.336) and dU is
in the range (1.720, 1.721).
c. d = 0.97 < dL . Therefore we reject H0 and conclude that
there is significant serial correlation.
d. OLS estimates are unbiased and consistent but not efficient (that
is, not BLUE). Hypothesis tests are invalid.
e. The list of reasons include:
- DW test can (and often does) lead to an inconclusive test.
- The test is not applicable to higher-order serial correlation.
- The test is not valid if the model contains lagged dependent
variables.
- If the number of variables is large, the DW table may not have
the critical values.
- DW test gives critical values only for a limited set of levels of
significance. LM test and p-value
can be used for any value. However, some programs such as SHAZAM do
give p-values for the DW d and can be used.
f. First transform the model as follows:
ln(
Qt)
-

ln (
Qt-1) =
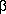 1
1 (1-

) +
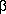 2
2 [ln(
Pt) -

ln (
Pt-1)]
+
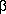 3
3 [ln(
Yt) -

ln (
Yt-1)]
+
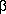 4
4 [ln(
ACCIDt) -

ln (
ACCIDt-1)]
+
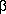 5
5 [ln(
FATALt) -

ln (
FATALt-1)] +
 t
t
Next fix

, at say
 1
1,
to be any any value between -1 and +1. Generate the variables
Qt* = ln(
Qt) -
 1
1 ln (
Qt-1),
Xt2*
= ln(
Pt) -
 1
1 ln (
Pt-1), and so
on to
Xt5*.
Then regress
Qt*
against a constant,
Xt2*
and so on to
Xt5*,
and compute the error sum of squares ESS. Vary
 1
1 between
-1 and +1 and choose the value

at which ESS is minimum. Then use this final

and transform to
obtain new
Qt*
etc. Finally regress
Qt*
against a constant,
Xt2*
and so on to
Xt5*to
complete estimates and related statistics.
Exercise 9.7
a. ut =  1ut-1
+
1ut-1
+  2ut-2
+
2ut-2
+  3ut-3
+
3ut-3
+  4ut-4
+
4ut-4
+  t
.
t
.
b. H0 :  1
=
1
=  2
=
2
=  3
=
3
=  4
= 0. H1
: At lesat one of the
4
= 0. H1
: At lesat one of the  's is not zero.
's is not zero.
c. Regress LHt
against a constant, LYt,
and Lrt.. Compute
 .
.
Then regress t against a
constant, LYt, Lrt,
t against a
constant, LYt, Lrt, t-1,
t-1, t-2,
t-2, t-3,
and
t-3,
and  t-4, either
using observations 5 through n
or using zero for the missing observations on the lagged
t-4, either
using observations 5 through n
or using zero for the missing observations on the lagged  t.
t.
d. Compute LM = nR2 = 40 R2
(or 36 R2 if you use
observations 5 through n)
where R2 is the
unadjusted R-square for the third step above.
e. Under the null hypothesis, LM has the chi-square distribution with 4
d.f.
f. Compute p-value = area to
the right of LM in 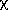 24. Reject H0 if p-value < 0.10.
24. Reject H0 if p-value < 0.10.
g. Forecasts are unbiased, consistent, but not efficient.
h. Generalized CORC procedure.
Step 1:
Regress
LHt
against a constant,
LYt,
and
Lrt..
Step 2: Compute

.
Step 3. Regress
 t
t
against a constant,
LYt,
Lrt,
 t-1
t-1,
 t-2
t-2,
 t-3
t-3,
and
 t-4
t-4, using
observations 5 through
n, and
obtain
 i
i,
i = 1 ... 4.
Step 4: Generate
LH*t =
LHt -
 1LHt-1
1LHt-1
-
 2LHt-2
2LHt-2
-
 3LHt-3
3LHt-3
-
 4LHt-4
4LHt-4
and similarly for
LY and
Lr.
Step 5: Regress
LH*t against a constant,
LY*t, and
Lr*t to get new estimates
of

,

and

.
Step 6: Go back to Step 2 and
iterate until the error sum of squares from Step 4 does not change by
more than some specified percent (say one percent).
Exercise 9.8
a. ut =  ut-1
+
ut-1
+  t
.
t
.
b. H0 :  = 0, H1 :
= 0, H1 :
 > 0.
> 0.
c. We have k' = 5 and n = 0. dL
= 1.230 and dU = 1.786. Because dL
< d < dU,
the test is inconclusive.
d. ut =  1ut-1
+
1ut-1
+  2ut-2
+
2ut-2
+  t
. H0 :
t
. H0 :
 1
=
1
=  2
= 0.
2
= 0.
e. n-2 = 38 and R2
= 0.687. Hence LM = 26.106. Under the null, LM has the chi-square
distribution with 2 d.f.
f. LM* = 13.816 < LM. Therefore we reject H0 and conclude that
there is significant second order correlation.
g. Generalized CORC procedure for AR(2).
Step 1:
Regress ln(
Qt)
against a constant, ln(
Kt),
ln(
Lt), ln(
At), ln(
Ft), and ln(
St).
Step 2: Compute
 t =
t =
ln(
Qt) -

-

ln(
Kt)
- ....
Step 3: Regress
 t
t
against
 t-1
t-1 and
 t-2
t-2
with no constant.
Step 4: Generate
Y*t = ln(
Qt) -
 1
1 ln(
Qt-1)
-
 2
2 ln(
Qt-2)
,
X*t2 = ln(
Kt) -
 1
1 ln(
Kt-1)
-
 2
2 ln(
Kt-2)
and similarly for the other explanatory variables.
Step 5: Regress
Y*t against a
constant and the
X*t variables and obtain new
estimates of the

's.
Step 6: Go back to Step 2 amd
iterate until the error sum of squares for Step 4 does not change by
more than some specified percent, say 0.01 percent.
Exercise 9.9
a. ut =  1ut-1
+
1ut-1
+  2ut-2
+
2ut-2
+  3ut-3
+
3ut-3
+  t
.
t
.
b. H0 :  1
=
1
=  2
=
2
=  3
= 0.
3
= 0.
c. LM = (n-3) R2
= 6.291.
d. Under H0, LM
has a chi-square distribution with 3 d.f.
e. For a 10 percent test, the critical LM* = 6.25139.
f. Since LM > LM*, we reject the null and hence conclude
that there is significant serial correlation.
g. Since serial correllation exists, OLS estimators are unbiased and
consistent, but not BLUE (that is, not efficient), and all tests are
invalid.
Exercise 9.10
a. SRt = RFRt +  MRt -
MRt -  RFRt + vt = RFRt (1-
RFRt + vt = RFRt (1- ) +
) +  MRt
+ vt . Therefore,
MRt
+ vt . Therefore,  1 = 0,
1 = 0,  2 =
2 =  , and
, and  3 = 1-
3 = 1- . The relevant restrictions are
. The relevant restrictions are  1 = 0 and
1 = 0 and  2 +
2 +  3 = 1.
3 = 1.
b. First regress SRt
against a constant, MRt
and RFRt, and save
the error sum of squares as ESSA.
Next generate Yt =
SRt - RFRt and Xt = MRt - RFRt. Then regress Yt against Xt without a constant
term ands save the error sum of squares as ESSB.
c. Compute Fc = [(ESSB - ESSA)/2] / [ESSA/(n-3)].
d. Under the null hypothesis, Fc
has the F-distribution with 2
and n-3 d.f.
e. The transformed model is:
(C)
SRt -
 SRt-1
SRt-1 =
 1
1 (1-

) +
 2 (MRt
2 (MRt -
 MRt-1
MRt-1) +
 3 (RFRt
3 (RFRt -
 RFRt-1
RFRt-1) +
 t
t .
Step 1: Choose

at a fixed value.
Then generate
SRt*
=
SRt -
 SRt-1, MRt*
SRt-1, MRt* =
MRt -
 MRt-1,
MRt-1,
and
RFRt*
=
RFRt -
 RFRt-1.
RFRt-1.
Step 2: Regress
SRt* against
a constant,
MRt*
, and
RFRt*
, and get
ESSC.
Step 3: Vary

at broad steps from
-0.99 through +0.99 say at steps of length 0.1. Choose the

that minimizes
ESSC at the starting point of a
CORC iteration.
Step 4: Repeat Step 2 after
using this

in Step 1 and
compute

.
Step 5: Get new estimate
 Step 6
Step 6: Repeat Steps 1, 2, 4,
and 5, using new

values and iterate
until

from two successive
iterations do not change more than say 0.001.
Step 7: Using this final

estimate Model C.
Exercise 9.11
a. ut =  1ut-1
+
1ut-1
+  2ut-2
+
2ut-2
+  3ut-3
+
3ut-3
+  4ut-4
+
4ut-4
+  t
.
t
.
H0 :  1
=
1
=  2
=
2
=  3
=
3
=  4
= 0.
4
= 0.
b. Breusch-Godfrey test.
- Regress LQ against a
constant, LP, and LY, and get
 .
.
- Generate
 t-1,
t-1, t-2,
t-2, t-3,
and
t-3,
and  t-4.
t-4.
- Regress
 t against
t against  t-1,
t-1, t-2,
t-2, t-3,
t-3,
 t-4,
constant, LPt, and
LYt, using only observations 5 through n.
Alternatively, place zeroes where the lag values are unknown.
t-4,
constant, LPt, and
LYt, using only observations 5 through n.
Alternatively, place zeroes where the lag values are unknown.
- Compute (n-4) R2
(nR2
if zeroes are inserted in the unknown lag values) where n is number of
observations and R2 is unadjusted R2
from (b.3). Under H0,
(n-4) R2
~
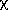 24.
24.
- Reject H0 if
P[
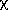 24
> (n-4) R2]
< level of significance or if (n-4)
R2
>
24
> (n-4) R2]
< level of significance or if (n-4)
R2
> 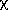 24(*), the
point on
24(*), the
point on 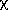 24 such that
the area to the right is equal to the level of significance.
24 such that
the area to the right is equal to the level of significance.
c. Generalized CORC procedure.
- Regress Regress LQ
against a constant, LP, and LY.
- Get
 .
.
- Generate
 t-1,
t-1, t-2,
t-2, t-3,
and
t-3,
and  t-4.
t-4.
- Regress
 t against
t against  t-1,
t-1, t-2,
t-2, t-3,
and
t-3,
and  t-4, [Note:
no constant term here, and no LPt
or LYt] and
get
t-4, [Note:
no constant term here, and no LPt
or LYt] and
get  1,
1,  2,
2,  3, and
3, and
 4.
4.
- Generate LQt*= LQt
-
 1 LQt-1 - ...
-
1 LQt-1 - ...
-  4 LQt-4, LPt*= LPt
-
4 LQt-4, LPt*= LPt
-  1 LPt-1 - ...
-
1 LPt-1 - ...
-  4 LPt-4, and LYt*= LYt
-
4 LPt-4, and LYt*= LYt
-  1 LYt-1 - ...
-
1 LYt-1 - ...
-  4 LYt-4.
4 LYt-4.
- Regress LQt*
against 1 -
 1
- ...
-
1
- ...
-  4 , LPt*, and LYt*, and get the next round of
estimates of
4 , LPt*, and LYt*, and get the next round of
estimates of  1,
1,  2, and
2, and  3.
3.
- Go back to Step 2 and iterate until ESS for Step 6 doesn't change
by more than some pre-specified number or percentage.
d. Estimates are biased, but consistent, and asymptotically efficient.
e. The error variance specification is  t2 =
t2 =
 0 +
0 +
 1 ut-12
+ ... +
1 ut-12
+ ... +  4 ut-42
.
4 ut-42
.
- Regress LQ against a
constant, LP, and LY.
- Compute
 .
.
- Generate
 2t-i, for i = 0, 1, ..., 4.
2t-i, for i = 0, 1, ..., 4.
- Regress
 2t against a constant,
2t against a constant,  2t-1, ...
2t-1, ...  2t-4, and compute the unadjusted
R2.
2t-4, and compute the unadjusted
R2.
- Compute LM = n R2.
Reject H0 if LM > 9.48773 which is the
point on
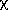 24 to the
right of which is the area 0.05.
24 to the
right of which is the area 0.05.
f. WLS estimation of ARCH model.
- Use the estimated
 i
from Step 4 above to obtain
i
from Step 4 above to obtain  .
.
- Compute
 .
.
- Generate LQt* = wt LQt,
LPt*= wt
LPt, and LYt*= wt
LYt.
- Regress LQt*
against wt , LPt* and LYt*, with no constant term.
[Up] [Home]
[Economics] [Memorial]
Updated March 2, 2009
noelroy AT mun.ca
 at which ESS is minimum. Then use this final
at which ESS is minimum. Then use this final  and transform to
obtain new Qt*
etc. Finally regress Qt*
against a constant, Xt2*
and so on to Xt5*to
complete estimates and related statistics.
and transform to
obtain new Qt*
etc. Finally regress Qt*
against a constant, Xt2*
and so on to Xt5*to
complete estimates and related statistics. at which ESS is minimum. Then use this final
at which ESS is minimum. Then use this final  and transform to
obtain new Qt*
etc. Finally regress Qt*
against a constant, Xt2*
and so on to Xt5*to
complete estimates and related statistics.
and transform to
obtain new Qt*
etc. Finally regress Qt*
against a constant, Xt2*
and so on to Xt5*to
complete estimates and related statistics. .
.  t against a
constant, LYt, Lrt,
t against a
constant, LYt, Lrt, t-1,
t-1, t-2,
t-2, t-3,
and
t-3,
and  t-4, either
using observations 5 through n
or using zero for the missing observations on the lagged
t-4, either
using observations 5 through n
or using zero for the missing observations on the lagged  t.
t. 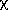 24. Reject H0 if p-value < 0.10.
24. Reject H0 if p-value < 0.10. .
. t
against a constant, LYt,
Lrt,
t
against a constant, LYt,
Lrt, t-1,
t-1, t-2,
t-2, t-3,
and
t-3,
and  t-4, using
observations 5 through n, and
obtain
t-4, using
observations 5 through n, and
obtain  i, i = 1 ... 4.
i, i = 1 ... 4. ,
,  and
and  .
. t =
ln(Qt) -
t =
ln(Qt) -  -
-  ln(Kt)
- ....
ln(Kt)
- ....  t
against
t
against  t-1 and
t-1 and t-2
with no constant.
t-2
with no constant. 1 ln(Qt-1)
-
1 ln(Qt-1)
-  2 ln(Qt-2)
, X*t2 = ln(Kt) -
2 ln(Qt-2)
, X*t2 = ln(Kt) -  1 ln(Kt-1)
-
1 ln(Kt-1)
-  2 ln(Kt-2)
and similarly for the other explanatory variables.
2 ln(Kt-2)
and similarly for the other explanatory variables. 's.
's. MRt -
MRt -  RFRt + vt = RFRt (1-
RFRt + vt = RFRt (1- ) +
) +  MRt
+ vt . Therefore,
MRt
+ vt . Therefore,  1 = 0,
1 = 0,  2 =
2 =  , and
, and  3 = 1-
3 = 1- . The relevant restrictions are
. The relevant restrictions are  1 = 0 and
1 = 0 and  2 +
2 +  3 = 1.
3 = 1. 1 (1-
1 (1- 2 (MRt -
2 (MRt - 3 (RFRt -
3 (RFRt - that minimizes ESSC at the starting point of a
CORC iteration.
that minimizes ESSC at the starting point of a
CORC iteration. in Step 1 and
compute
in Step 1 and
compute .
.
 values and iterate
until
values and iterate
until  from two successive
iterations do not change more than say 0.001.
from two successive
iterations do not change more than say 0.001. estimate Model C.
estimate Model C. .
. t-1,
t-1, t-2,
t-2, t-3,
and
t-3,
and  t-4.
t-4. t against
t against  t-1,
t-1, t-2,
t-2, t-3,
t-3,
 t-4,
constant, LPt, and
LYt, using only observations 5 through n.
Alternatively, place zeroes where the lag values are unknown.
t-4,
constant, LPt, and
LYt, using only observations 5 through n.
Alternatively, place zeroes where the lag values are unknown.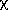 24.
24. 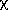 24
> (n-4) R2]
< level of significance or if (n-4)
R2
>
24
> (n-4) R2]
< level of significance or if (n-4)
R2
> 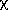 24(*), the
point on
24(*), the
point on 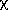 24 such that
the area to the right is equal to the level of significance.
24 such that
the area to the right is equal to the level of significance. .
. t-1,
t-1, t-2,
t-2, t-3,
and
t-3,
and  t-4.
t-4. t against
t against  t-1,
t-1, t-2,
t-2, t-3,
and
t-3,
and  t-4, [Note:
no constant term here, and no LPt
or LYt] and
get
t-4, [Note:
no constant term here, and no LPt
or LYt] and
get  1,
1,  2,
2,  3, and
3, and
 4.
4. 1 LQt-1 - ...
-
1 LQt-1 - ...
-  4 LQt-4, LPt*= LPt
-
4 LQt-4, LPt*= LPt
-  1 LPt-1 - ...
-
1 LPt-1 - ...
-  4 LPt-4, and LYt*= LYt
-
4 LPt-4, and LYt*= LYt
-  1 LYt-1 - ...
-
1 LYt-1 - ...
-  4 LYt-4.
4 LYt-4. 1
- ...
-
1
- ...
-  4 , LPt*, and LYt*, and get the next round of
estimates of
4 , LPt*, and LYt*, and get the next round of
estimates of  1,
1,  2, and
2, and  3.
3. t2 =
t2 =
 0 +
0 +
 1 ut-12
+ ... +
1 ut-12
+ ... +  4 ut-42
.
4 ut-42
. .
. 2t-i, for i = 0, 1, ..., 4.
2t-i, for i = 0, 1, ..., 4. 2t against a constant,
2t against a constant,  2t-1, ...
2t-1, ...  2t-4, and compute the unadjusted
R2.
2t-4, and compute the unadjusted
R2. 24 to the
right of which is the area 0.05.
24 to the
right of which is the area 0.05. i
from Step 4 above to obtain
i
from Step 4 above to obtain  .
. .
.